Puzzles & casse-tête en bois gratuits à fabriquer, construire soi-même

X-cube un jeu de cubes pour adulte qui n'a rien à voir avec le X de pornographique!

les X-cubes sont nés  d’une idée de Henry Lemarchal dit  HLM sur les forums du bois. Ce passionné du bois de notre association d'Evry est aussi un participant du forum de l'air du bois c'est là que j'ai découvert ses X-cubes! qu'il nome plus simplement des "cubes".

ils ne forment pas à proprement parlé un casse-tête mais plutôt un jeu de cubes, mais surtout un bon exercice pour le travail du bois: choix du bois, carrelet rectangulaire (mais finalement une figure plutôt cubique), coupes biaises, collage et tourillons, finitions à choisir, etc...

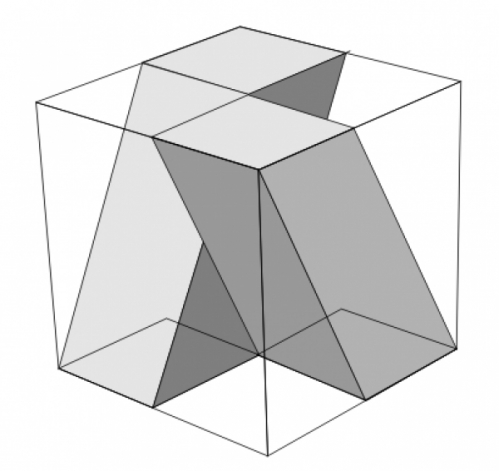
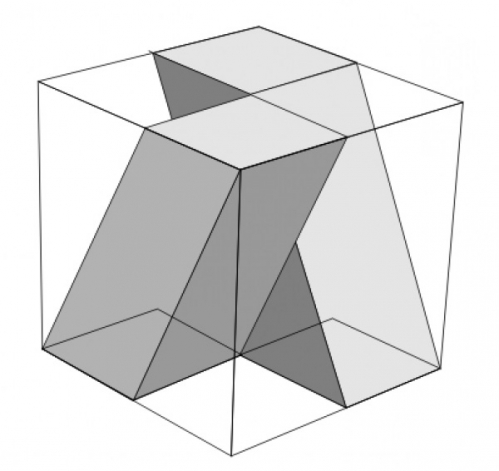
le principe de base est  simplissime mais très original on part d'un cube et on y découpe une figure simple mais nouvelle en forme de X:

Il faut remarquer qu'il existe des droits et des gauches selon la façon de décomposer le cube qui sont comme les mains gauche et droite non superposables par rotations mais l'image l'un de l'autre dans un miroir (on dit aussi énantiomorphe ou chiral pour cette  propriété).

Si on part d'un cube pour les fabriquer on va systématiquement perdre 50% du matériau bois.Par contre en partant d'un  carrelet carré le coté découpé ne sera pas un carré mais un rectangle il faut donc un carrelet rectangulaire pour obtenir une coupe biaise qui elle, sera carré vue en coupe biaise.

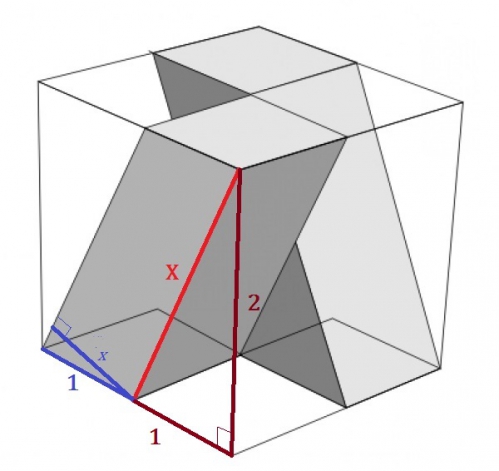
Si on considère que le coté du cube fait 2 unités de coté, le carrelet a lui un coté d'une unité et l'autre un coté de largeur x et une longueur de X.

On a les relations suivantes en raison du théorème de Pythagore et Thalès:

X²=2²+1²=5 soit X=√5  relation entre hypoténuse et cotés adjacents

et donc  x/1=2/X=2/√5=0.8944. triangles semblables

Il faut donc partir d'un carrelet rectangulaire (ou généralement carré) et raboter un coté pour obtenir un rapport de 0.8944 entre ces deux cotés. On ne perd alors que 11% maximum du bois.

Ce qui permet d'envisager les possibilités approchantes suivantes pour les dimensions des cotés de la section du carrelet en mm:

29*26=0.8965 pour un cube de 58 mm de coté

38*34=0.89473                              76 mm

35*31.3=0.8942                             70 mm

36*32.2=0.8944                             72 mm

Il reste à fabriquer un berceau de coupe avec un guide pour scie japonaise et le débit devient plus facile et surtout régulier.

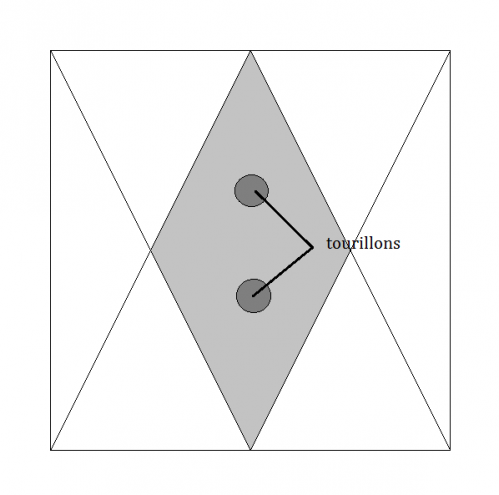
Puis l'assemblage dans un mannequin de collage où l'on peut aussi éventuellement percer des trous traversants pour introduire deux tourillons destinés à éviter les décollages lors des manutentions et les chutes inévitables.

plus il y a de cubes en X plus le jeu permet de variations y compris éventuellement en utilisant des gauches et droits (mais Henry pense que ce n'est pas indispensable).

Il a dénombré plus d'une vingtaine d'arrangements et pense n'avoir pas tout trouvé. Pour vous laisser le plaisir de les chercher en voici quelques exemples:

                 

Une sorte de brique élémentaire pour inventer toutes sortes de claustras et formes diverses de plan ou d'assemblages en polygones, etc...

un exemple d'utilisation de la même forme de base pour en faire un pot à crayons original

Il suffit de faire varier l'exercice. Par exemple partir d'un hexagone et de carrelets triangulaires pour inventer d'autres jeux de briques élémentaires amusantes qui renouvellent le plaisir enfantin de jouer aux cubes de construction et surtout de trouver un prétexte pour travailler le bois et son imagination.