Pocoloco ou un peu fou
Pocoloco
Un nom qui signifie un peu fou en espagnol.
Un casse-tête de Vaclav Obsivac un créateur de casse-tête d'origine tchèque plus connu sous le pseudo de Vinco.
Un casse-tête à la fois relativement simple à construire, esthétique, facile à résoudre au montage et un peu plus hermétique au démontage et très facile à mémoriser.
Du pur bonheur pour le travail du bois et de faible difficulté pour les amateurs de casse-tête!
On part d'un carrelet que l'on coupe sur une diagonale dans un berceau. Le berceau est composé de deux coupes à 45° assemblées sur une planche.
On obtient deux longueur dont la section est un triangle rectangle et isocèle avec un angle droit au sommet et deux angles de 45° à chaque extrémité de l’hypoténuse.
On passe les deux moitiés du carrelet au rabot ou à la ponceuse calibreuse sur un berceau (qui peut être le même assemblage de 2 coupe à 45° s'il est assez long avec la face la plus grande orientée vers le haut et fixée par butées) pour parfaitement égaliser et régulariser cette face la plus large et avoir une largeur uniforme. Personnellement je l'ai simplement obtenue à la ponceuse.
on recoupe perpendiculairement à la scie à ruban ou dans une boite à coupe avec la scie japonaise et une butée réglable pour obtenir 18 morceaux prismatiques identiques avec la face parfaitement carré.
On vérifie donc l'égalité des cotés et l'orthogonalité au pied à coulisse et à l'équerre.
On assemble par collage les éléments trois par trois pour obtenir six pièces identiques au total comme la photo suivante avec un banc de collage à faces perpendiculaires.
Avec de la colle vinylique, je ne le met pas sous presse, tenu seulement entre les doigts quelque dizaine de secondes, le temps que ça "ventouse" par capillarité dans les pores du bois, par contre il faut bien attendre 24h de séchage avant de solliciter les collages sinon ça se désarticule facilement.
par contre l'épaisseur de la colle peut jouer sur les côtes donc après essais, rectification par ponçage léger en fonction du dosage de colle.
ATTENTION MAUVAIS SENS!
Surtout ne pas se tromper sinon faut tout décoller et refaire comme moi et c'est peut-être pour ça que je suis tombé sur la bonne côte puisque j'ai fais disparaître les traces de colle et donc diminué la côte initiale.
BON SENS
L'assemblage est trivial et auto-bloquant si les côtes sont justes. C'est donc un casse-tête que l'on ne peut pas vernir car les jeux disparaîtraient et le montage deviendrait impossible, on peut utiliser du roubio comme dans l'article " t’es mal rangé". La première pièce (qui peut être n'importe laquelle) à démonter demande un peu de force et d'astuce dans les prises et des repères pour la tirer (je fais quatre petits points noirs au crayon mine sur celle qui glisse le plus facilement).
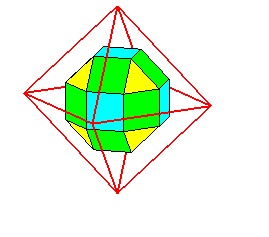
Le nom de sa forme composé de 6 carrés 12 rectangles et 8 triangles équilatéraux:
le cube ou octaèdre tronqué aux arêtes et aux sommets.

Et si on le construit à partir de pièces débitées dont la section est un triangle équilatéral (60°) et non un triangle droit (90°).
On transforme les rectangles en carrés et on obtient le rhombicuboctaèdre de 18 carrés et 8 triangles équilatéraux.
Pour les polyèdres réguliers on distingue 4 types de troncatures conduisant à des polyèdres ayant encore certaines régularités :
Toutes ces animations sont extraites de mathcurve à la page polyèdre chanfreiné
polyèdre tronqué aux sommets

Chaque sommet est tronqué par un plan perpendiculaire à l'axe de la rotation laissant le polyèdre invariant, créant S faces polygonales régulières d'ordre le degré des sommets
polyèdre tronqué aux arêtes

Chaque arête est tronquée par un plan parallèle à l'arête et perpendiculaire au plan médiateur des deux faces correspondantes, créant A faces hexagonales.
polyèdre tronqué aux arêtes et aux sommets

Combinaison des deux précédentes ; il y a création de S faces polygonales régulières d'ordre le degré des sommets et de A faces rectangulaires.
polyèdre tronqué aux arêtes et fortement tronqué aux sommets

Combinaison des deux premières ; il y a création de S faces polygonales régulières d'ordre le double du degré des sommets et de A faces rectangulaires ; les F faces doublent leur nombre d'arêtes.
Ces constructions peuvent être étendues aux cas où on obtient des polyèdres étoilé :

Inscrivez-vous au blog
Soyez prévenu par email des prochaines mises à jour
Rejoignez les 190 autres membres